진자를 움직이는 힘

중력에 의한 장력

물리학에서 장력은 두 물체를 이은 끈에 걸리는 힘입니다. 일반적으로 장력은 끈의 양 끝에서 끈의 중심 방향을 향하는 것으로 계산합니다.
길이 $l$인 진자를 각도 $\theta_m$ 만큼 들어 올렸다가 놓은 진자를 생각해 봅시다. 끈의 질량은 없는 것으로 가정합니다.

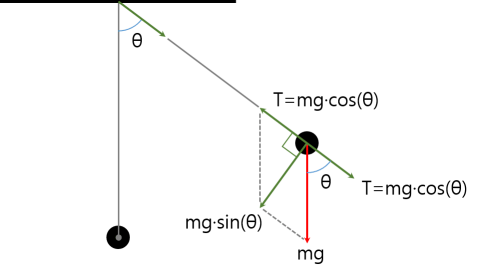
진자에 가해지는 힘의 원천은 중력(=$mg$)입니다. 이 중력은 다음의 두 힘으로 분해될 수 있습니다.

• ‘중력에 의한 장력’ T = $mg\cdot cos\theta$
• ‘중력에 의해 진자를 움직이는 힘’ = $mg\cdot sin\theta$ (= T와 mg의 벡터합)

진자의 구심력

진자가 최고점에서 내려오면 추가로 하나의 힘이 더 생겨납니다. 진자의 회전운동을 유지하기 위한 구심력입니다.
진자의 길이가 $l$이고, 속력이 $v$인 경우 구심력은 다음과 같습니다.

$$F=\frac{mv^2}{l}$$

구심력도 ‘중력에 의한 장력’과 마찬가지로 끈의 끝에서 중심을 향합니다.

줄에 가해지는 전체 장력

줄에 가해지는 전체 장력은 다음과 같이 계산할 수 있습니다.

$$\begin{align} 전체\,장력 &= 중력에\,의한\,장력 \, + \, 구심력 \\&= mg \cdot cos \theta \, + \, \frac{mv^2}{l} \end{align}$$

위의 식에서, $v$와 $l$을 $\theta$에 관련된 식으로 간단하게 만들어 보겠습니다.
최고 진폭이 $\theta_m$이고 현재 진폭이 $\theta$인 진자를 생각해 봅니다.

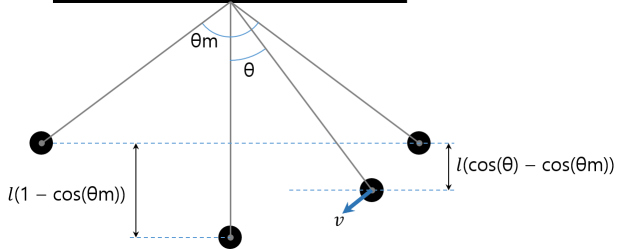
에너지 보존 법칙에 의해, 증가한 운동 에너지는 줄어든 위치 에너지와 같습니다.

$$\frac{1}{2} mv^2 = mgl(cos \theta – cos \theta_m ) \\ \therefore v^2 = 2gl(cos \theta – cos \theta_m )$$

위의 식을 장력에 대입해 보면,

$$\begin{align} 전체\,장력 &= 중력에\,의한\,장력 \, + \, 구심력 \\&= mg \cdot cos \theta \, + \, \frac{m \cdot 2gl(cos \theta – cos \theta_m )}{l} \\&= mg \cdot cos \theta \, + \, 2mg(cos \theta – cos \theta_m ) \\&= mg(3cos \theta – 2cos \theta_m ) \end{align}$$

가 됩니다.