Definite integral
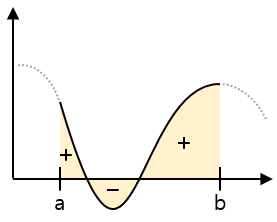
In the 2D coordinate plane, a definite integral is a way to find the area of a graph.
In a rectangle, the only simple way to get the area is the multiplication of width and height.
If the shape is not constant, you can not get the area by simple multiplication. When a section of the graph is defined, we use a definite integral to find that section’s area.
The mathematical definition of the integral is :
Try to divide the sections so that the width of the sections is infinitely small. When this sum is always close to a constant value, we define that value as the definite integral of a to b.
\[ (Area) =\, \int_{a}^{b} f(x) \; dx \]
How to definite integral
To integrate, you first need to know the derivative.
Please searching the internet about the differential method.
Integral can be said to be the inverse of the derivative. Suppose a function f(x) is the derivative of F(x) with ‘x’. In this case, integrating f(x) results in ‘F(x) + C(integral constant)’.
Whatever the integration process, if you can integrate the function, you can get the definite integral value as :
\[ \int_{a}^{b} f(x) \; dx \, = \, F(b) – F(a) \]
Examples of definite integrals often used in Physics
| Speed-time graph |  |
Area = Distance traveled for the duration of the interval
|
|---|---|---|
| Acceleration-time graph | 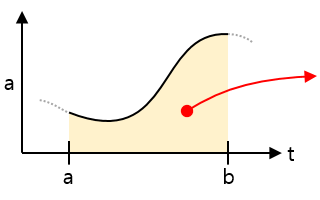 |
Area = The rate of change of speed over the duration of the interval
|
| Force-time graph | 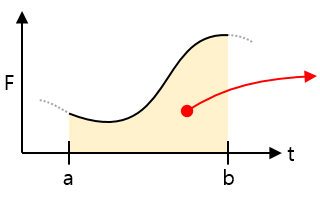 |
Area = The amount of received impact (momentum) during the time of the interval
|
| Force-distance graph | 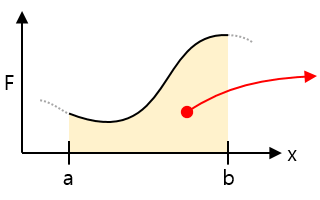 |
Area = The amount of work done to move the distance of the section, the energy stored or released in the spring |